5.1 Overview¶
Algorithm description¶
This script performs automatically the photometry of all detected objects on a large number of images. It has been written to detect variable stars in fields containing possibly thousands of stars.
In particular:
- the script works only for fixed objects (it works for stars but not for asteroids).
- the images do not need to be co-aligned: the script takes care of calculating the shifts between the images.
- the user defines how many stars he want to measure (say N), and the script detects the N brightest objects.
- then the photometry is performed with an aperture with fixed size. The photometry cannot be optimal since the best disk size is not the same for every object. But the accuracy is already pretty good.
- the script works for very crowdy fields (number of stars up to >30000) and a large number of images (tested up to >1000).
- it makes use of parallel computing to use all the processors and reduce the calculation time. With a 4-processors computer at 2.40GHz, the script calculates the photometry of 2000 stars over 100 images in 60 seconds.
- once all magnitudes have been calculated, they are stored in a text file
- a second script can be used to read and display the measured magnitudes and statistics, to allow to identify the outsiders and check their lightcurve
Lightcurve statistics¶
Given the very large amount of data produced by this script, the use of statistics is mandatory to search variable stars. Three statistics figures are calculated by the script for each star:
- the average magnitude
- the standard deviation of the magnitude values, called here “global noise”
- the same standard deviation but calculated after filtering out the slow oscillations of the magnitudes (high pass filter), called “local noise”
The average and standard deviation of the magnitude values are calculated with:
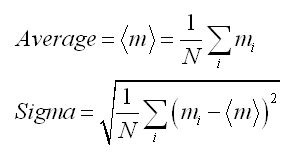
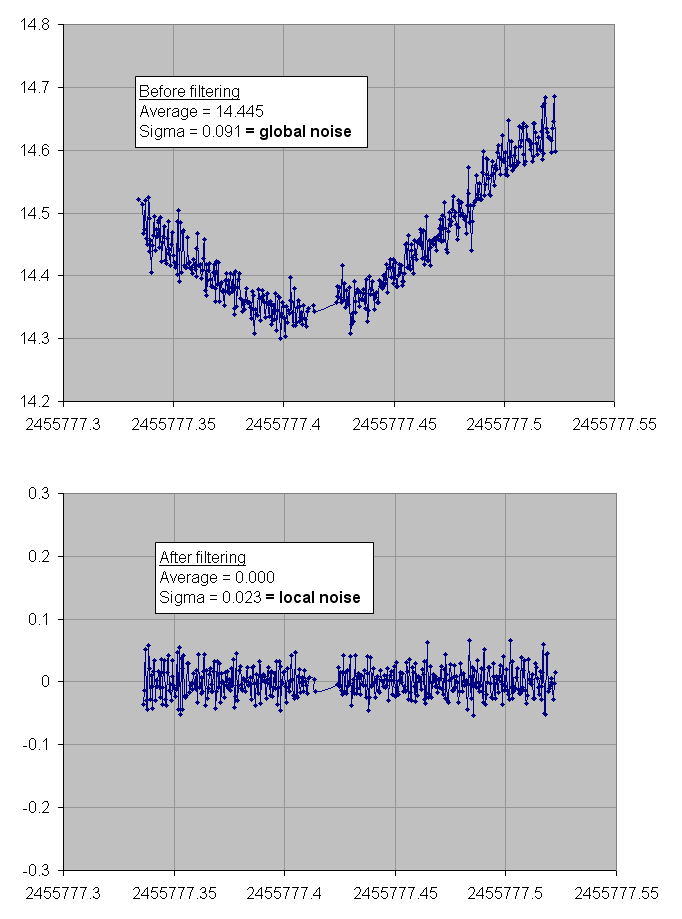
The difference between “global noise” and “local noise” is illustrated below. The filtering of the slow oscillations to calculate the “local noise” is done with a moving averaging window. The corresponding filter spectral response is a sinc(x) function which is in fact far from being a perfect high pass : one could imagine to use better filters. Nevertheless the otained “local noise” provides a very good estimate of the noise in the lightcurve.
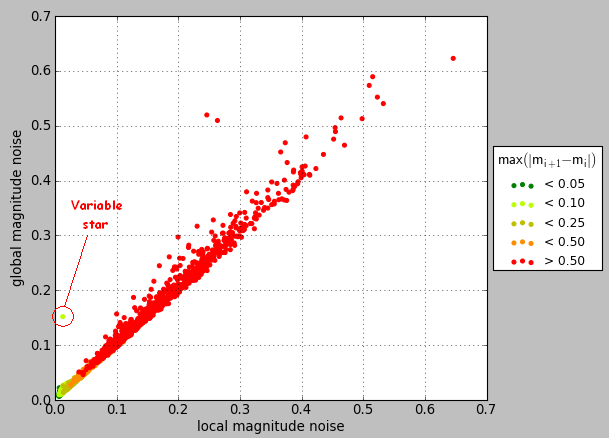
Finding variable stars¶
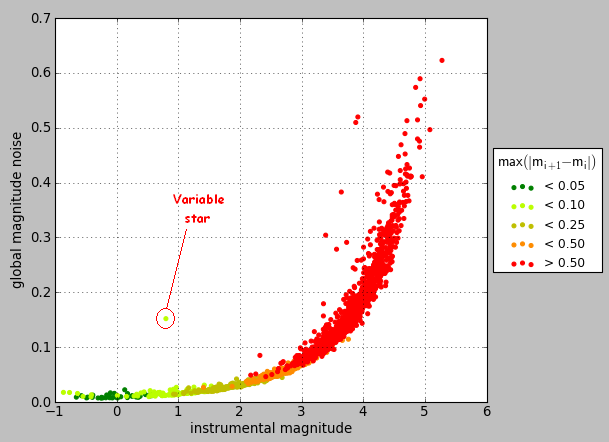
To search variable stars, we are using two approaches. The first one is based on a plot of the global noise as a function of magnitude.
The second method is based on a plot of local noise as a function of global noise. It is visible, on the curve, that the global noise is always higher than local noise. This comes from the filtering operation, which removes the “low frequency noise”.